The goal of this written assignment is to first do some exercises in radiometry, and then to work on camera models. The mathematics that you derive for camera models will be used in your next programming assignment.
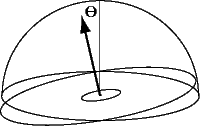
1. Assume the sky has constant radiance L over the entire upper hemisphere (it is a perfectly cloudy day). In class, we showed that a constant radiance hemispherical source would contribute irradiance E = π L to a point on the ground.
Suppose at some point on the terrain the ground plane is tilted by an angle θ with the respect to the horizon. These means a angular wedge of the hemispherical sky will not be visible at that point because parts of the sky are below the local horizon of the surface.

What is the irradiance E at this point?
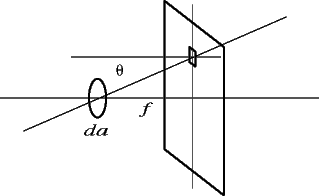
2. A real optical system exhibits vignetting. Vignetting causes the exposure to vary from a maximum at the center of the image to a lesser value at the edges.
Assume you have a camera with a infinitesimal disk aperture da. Behind the aperture at distance equal to the focal length f is the film plane. Show that the irradiance on the film plane goes as the cos^4 θ.
3. In computer graphics, camera projections are represented by 4x4 matrices. In fact, lrt uses a 4x4 matrix to model the camera.
First, describe the method that lrt uses to generate eye rays given a 4x4 camera projection matrix. The camera transformation module of lrt is documented in chapters 1 and 5 of the lrt book.
Second, how would you modify this method for generating eye rays if you wanted to model a camera with a finite aperture? Please describe the steps in words, and also mathematically. [Hint: Read carefully the discussion of depth of field in Rob Cook's chapter in the Introduction to Ray Tracing Book].
The programming assignment will involve implementing this effect and demonstrating depth of field and motion blur.
Copyright © 2001 Pat Hanrahan